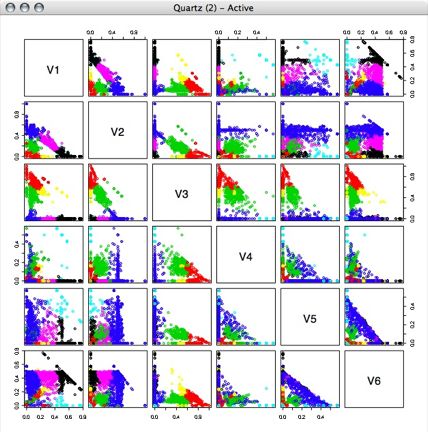
Problem
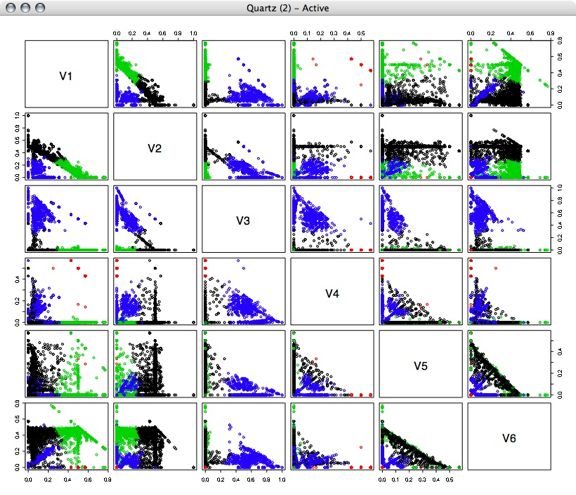
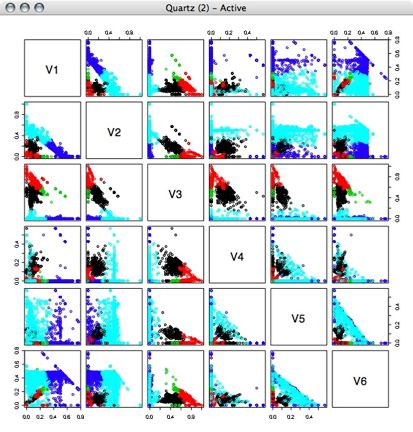
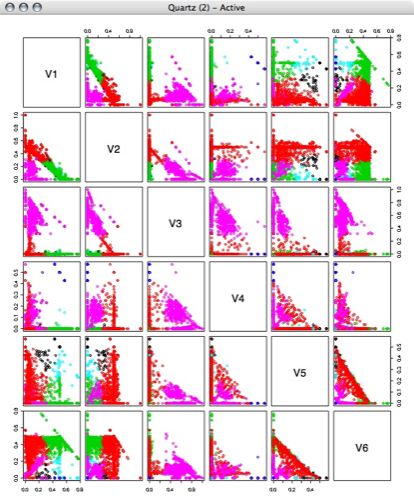
We are interested in finding out whether there are a finine number of distinct behavior types within the phase response curve (PRC) data. We used the 10 time points of the data as the 10 "features" or dimensions of the data. We decided to use principal components analysis (PCA) on the data in order to reduce the dimension of the data to something that would be easier to work with.
Wikipedia gives a concise description of PCA:
In statistics, principal components analysis (PCA) is a technique that can be used to
simplify a dataset; more formally it is a linear transformation that chooses a new
coordinate system for the data set such that the greatest variance by any projection
of the data set comes to lie on the first axis (then called the first principal component),
the second greatest variance on the second axis, and so on. PCA can be used for reducing
dimensionality in a dataset while retaining those characteristics of the dataset that
contribute most to its variance by eliminating the later principal components (by a more
or less heuristic decision). These characteristics may be the "most important", but this
is not necessarily the case, depending on the application.
A good paper and matlab tutorial for PCA is written by Jonathon Schlens.
By using principal components analysis on the data we were able to reduce the dimensions from 10 to 2 while still preserving most of the variance. This allowed us to then re-project the data into two dimensions and look for large groups of similar behavior (results below).
Next we intend to try some clustering algorithms on this data in order to define the areas that have a lot of similar behavior and then use them with John's dimension stacking tool to see whether the prominantly similar areas of the PRC behavior are interestingly distributed in conductance space.
Technique and Results
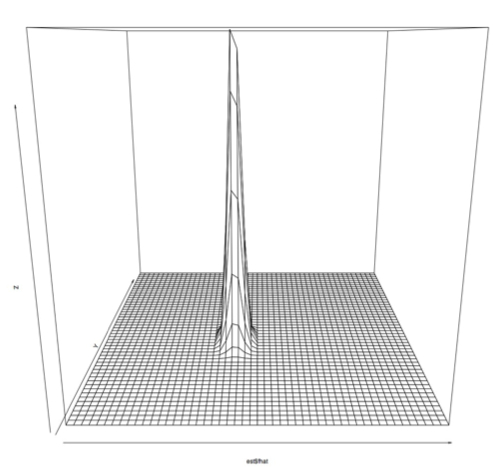
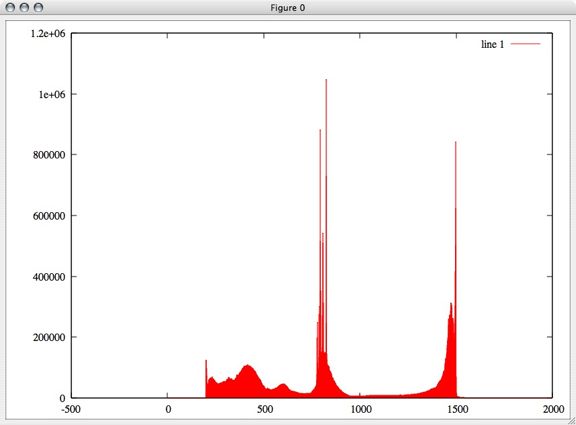
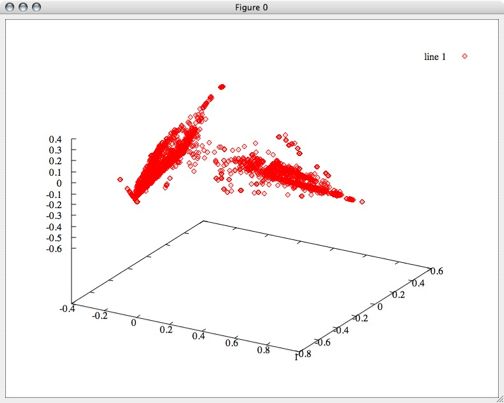
First, we ran principle component analysis on the entire PRC set. Variance was very high, but this included outliers outside of the -1 to 1 phase shift that the PRC data is supposed to contain. We projected the data using the first 2 principle components, and made a plot showing how many samples were at each point. Using a single principal component we would have been able to preserve 92% of the variance, while using the first two principle components preserves 96% of the variance. (Adding the 3rd component brought the variance preserved up to 97% and the preservation continued to increase only slowly until 100% was preserved with all 10 dimensions) However, since we had a few outlying points as far out as -1000 and 700, this representation wasn't very useful:
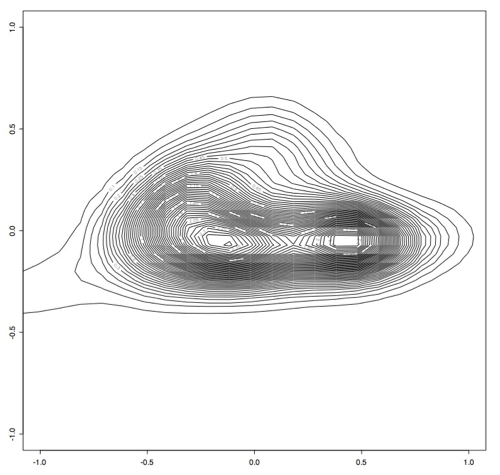
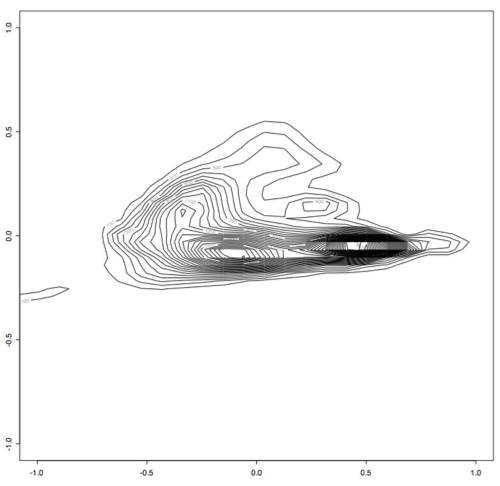
Next, we filtered out any of the original data that contained points outside of the perscribed -1 and 1 range and ran principle component analysis on this slightly smaller data set. This produced smaller variance as expected, since the data was all within a much smaller range. Again using the first two principle components, we projected this data into 2 dimensions and made several plots that show how many samples appear at each point in 2d space. [I am computing the variance preservation and will add it soon.]
This is the R code I used:
> x <- read.table("~/Desktop/smallsignals", header = TRUE)
> est <- bkde2D(x, bandwidth=c(0.1,0.1))
> contour(est$x1, est$x2, est$fhat)
Which produces this contour plot:
As you can see here, there seem to be two main "types" of PRC behavior. One of the next steps will be to find out what's in these two areas that makes them so distinct.
I also plotted this data using a 3D perspective with this code:
> persp(est$fhat)
Which produces this sort of plot:
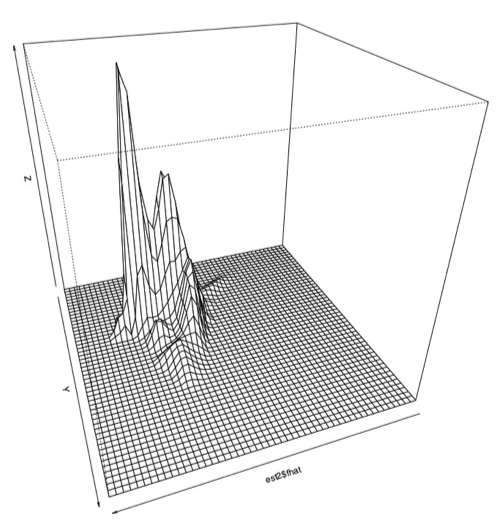
Zoomed in:
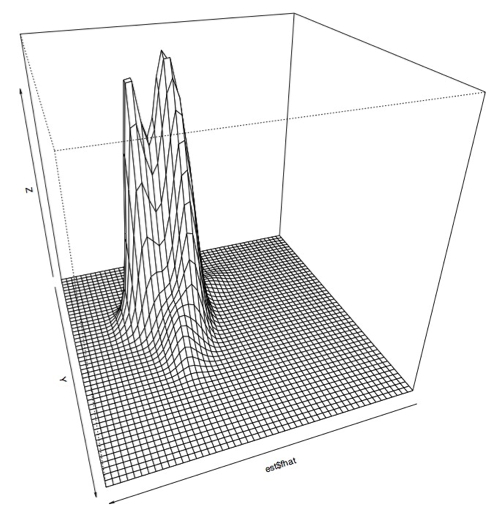
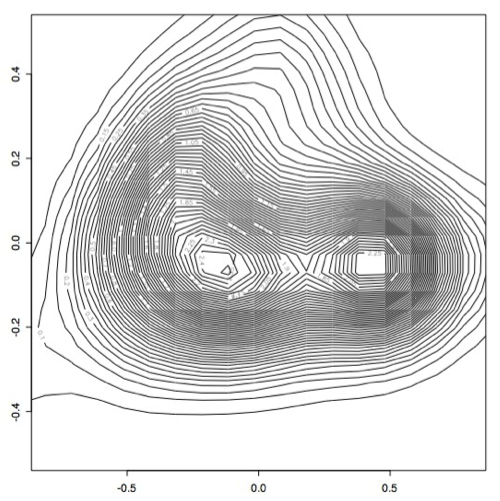
However, it became apparent that the [0.1,0.1] bandwidth that we used to begin with did not capture all of the peaks exactly because there were some smaller peaks. After experimenting with several bandwidth sizes varying between 0.1 and 0.000001, it became apparent that the plots did not change much once you made bandwidth smaller than 0.001, so I decided to use this as the "best" bandwidth size for this data.
As you can see, the data has a slightly different shape:
I think there may actually be more like three or four different classes, but only two very large classes.
Results Analysis
The next thing I wanted to do was see what exactly was represented by these high density areas that we have been assuming are "classes" of PRC behavior.
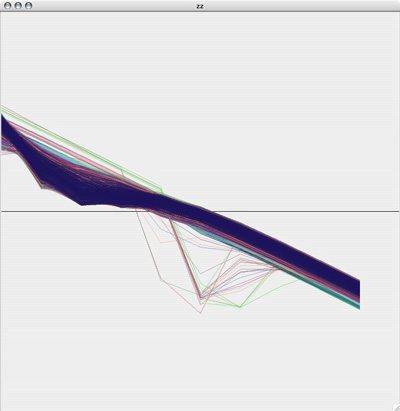
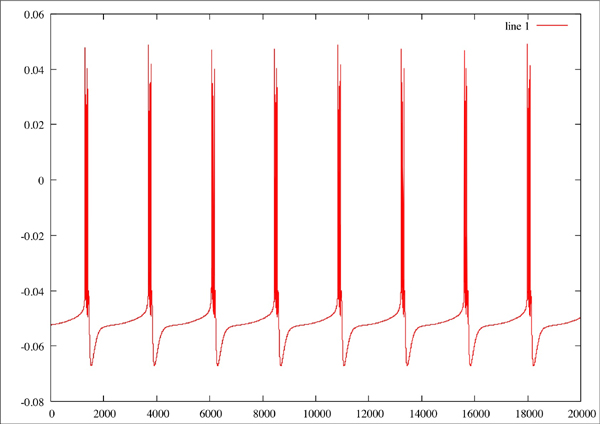
Plotting several hundred thousand of the PRC plots by themselves gives you a plot that looks a lot like this:
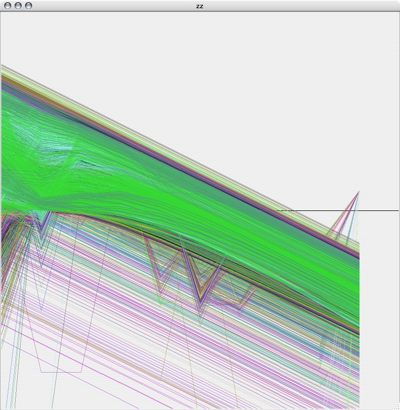
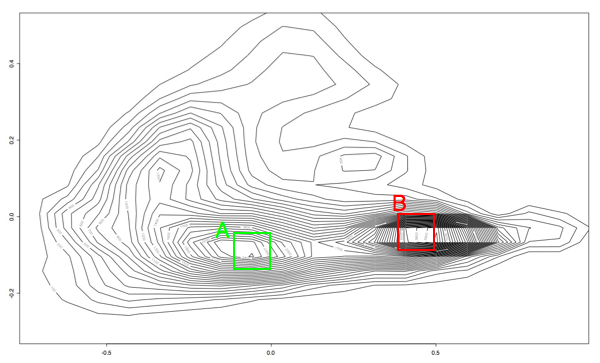
Kind of pretty, but not very useful. So the next thing I did was write a quick and dirty octave script to make collections of PRC plots that fell into these two ranges. The boxes are just eyeballed in a graphics editing program, so they aren't the last word in accuracy, but it let me at least get an idea of the area:
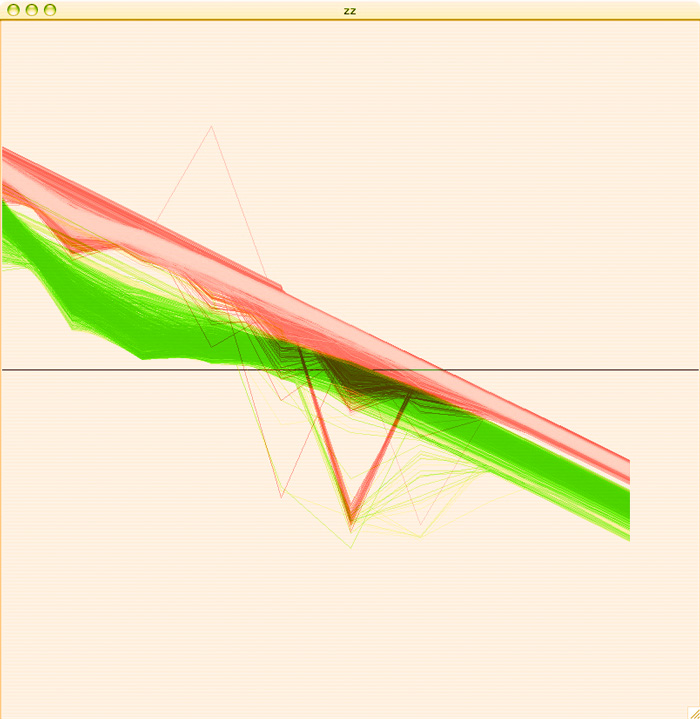
The plots from the "A" area all plotted together look something like this:
While the plots in the "B" region look like this:
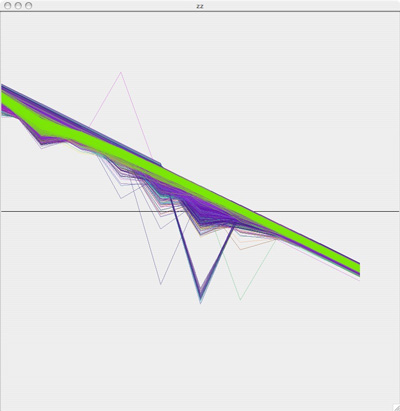
To get a more accurate idea of how separate these two groups are, I colored the A plots green, the B plots red, added some transparency and overlaid the two graphs so that we could see where these plots are in relation to each other:
I am pretty pleased with the separation of behaviors, considering that this is just a first pass. Hopefully with some clustering we'll be able to get some more acurate separation of behaviors than I am able to get by hand.